需要前置了解的知识:线代基本知识、旋转矩阵(Rotation Matrix)和变换矩阵(Transformation Matrix)、DH(Denavit & Hartenberg)的Craig表示法。在学习机械臂的逆运动学(Inverse Kinematics,IK)时,一定是从已知的变换矩阵解算到每一个Joint Angle(即$\theta$角)的代数方法最令人头大,这篇笔记尽量用通俗的方法简单讲解一下这个计算过程,即大名鼎鼎的Pieper’s Solution,防止以后遗忘。
Pieper的精妙之处在于,他发现如下图所示的PUMA手臂6个转轴,只有前三个转轴决定手腕中心的位置,而后三个转轴交于一点,即其Frame共原点。这样一来,我们可以分开来先计算$\theta_1$、$\theta_2$、$\theta_3$,再计算$\theta_4$、$\theta_5$、$\theta_6$,而后三个只要反解简单的欧拉角变换即可。
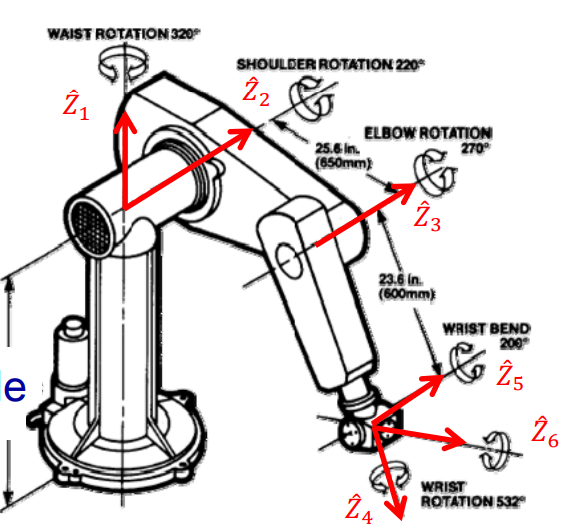
$\theta_1$、$\theta_2$、$\theta_3$解算
我们做解算的总体思路是,我们需要在复杂的矩阵运算中不断消元,消灭$\theta_1$和$\theta_2$,最终建立一个关于$\theta_3$的方程解出$\theta_3$,这是第一步。然后将$\theta_3$回代,算出$\theta_1$和$\theta_2$,这是第二步。第一步消元是最具有挑战性也是最精妙的部分。
消元
在计算之前,我们先通过物理关系思考一下怎么消元。针对IK运算,我们已知的是${}^{6}_{0} T$(Frame6到Frame0的变换矩阵),由于转轴相交,其物理意义可看作Joint4的位置,即手腕中心,我们需要得出的是三个角的角度。可以想象到,从肘关节(Joint3)的视角看,只有$\theta_3$会导致手腕位置改变,即可以把其表示成$\theta_3$的函数;同样地,从肩膀(Joint2)的视角看,只有$\theta_2$和$\theta_3$会导致手腕位置改变,可以把其表示成$\theta_2$和$\theta_3$的函数。有意思的是,无论我的$\theta_1$怎么变化(即腰怎么扭),其不影响肩膀到手腕中心的距离和手腕中心相对地面的高度,这两个关系消去了$\theta_1$,两个方程两个未知数,得到最终的$\theta_2$和$\theta_3$。下面开始正式计算,我们会发现通过计算可以在数学上验证上面的意识流过程。
首先,我们知道${}^{6}_{0} T$,并且其第四列是从Frame0原点指向Frame6原点的向量,但加了一行1,形如$\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$,记作${}^0 P_{6 \text{ORG}}$。由于转轴相交,原点位置相同,其显然等于${}^0 P_{4 \text{ORG}}$。我们现在试图用$\theta_1$、$\theta_2$、$\theta_3$来表示其中的已知的三个$x$、$y$、$z$常数,我们知道:
$$ \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = {}^0 P_{4 \text{ORG}} = {}_1^0 T {}_2^1 T {}_3^2 T {}^3 P_{4 \text{ORG}} $$通过DH Craig几何关系可得:
$$ {}^{i-1}_{i} T = \begin{bmatrix} c\theta_i & -s\theta_i & 0 & a_{i-1} \\ s\theta_i c\alpha_{i-1} & c\theta_i c\alpha_{i-1} & -s\alpha_{i-1} & -s\alpha_{i-1} d_i \\ s\theta_i s\alpha_{i-1} & c\theta_i s\alpha_{i-1} & c\alpha_{i-1} & c\alpha_{i-1} d_i \\ 0 & 0 & 0 & 1 \end{bmatrix} $$上式除了$\theta$以外都是常数,$s$、$c$是$\sin$、$\cos$的通用缩写,$s_n$、$c_n$为$\sin\theta_n$、$\cos\theta_n$的缩写。其中代入有${}^3 P_{4 \text{ORG}} = \begin{bmatrix}a_3 \\-d_4 s\alpha_3 \\d_4 c\alpha_3 \\1\end{bmatrix}$,则${}^0 P_{4 \text{ORG}}$可表示为${}_1^0 T {}_2^1 T {}_3^2 T \begin{bmatrix} a_3 \\ -d_4 s\alpha_3 \\ d_4 c\alpha_3 \\ 1 \end{bmatrix}$,接下来就是繁琐的矩阵乘法运算,为了表达方便,我们使用剥洋葱法,一层一层定义函数防止算式过长,对应前面意识流中不同视角看手腕中心。下面代入${}^{i-1}_{i} T$计算,定义$f(\theta_3)$和$g(\theta_2,\theta_3)$:
$$ ^0 P_{4 \text{ORG}} = {}_1^0 T {}_2^1 T {}_3^2 T\begin{bmatrix}a_3 \\-d_4 s\alpha_3 \\d_4 c\alpha_3 \\1\end{bmatrix} = {}_1^0 T {}_2^1 T \begin{bmatrix} f_1(\theta_3) \\ f_2(\theta_3) \\ f_3(\theta_3) \\ 1 \end{bmatrix} = {}_1^0 T \begin{bmatrix} g_1(\theta_2,\theta_3) \\ g_2(\theta_2,\theta_3) \\ g_3(\theta_2,\theta_3) \\ 1 \end{bmatrix}= \begin{bmatrix} c_1 g_1 - s_1 g_2 \\ s_1 g_1 + c_1 g_2 \\ g_3 \\ 1 \end{bmatrix} $$前面提到肩膀到手腕中心的距离与$\theta_1$无关,为了计算方便,我们就算这一距离的平方,并简记为$r$:
$$ \begin{align*} r &= (c_1 g_1 - s_1 g_2)^2 + (s_1 g_1 + c_1 g_2)^2 + g_3^2 \\ &= (c_1^2 g_1^2 - 2 c_1 s_1 g_1 g_2 + s_1^2 g_2^2) + (s_1^2 g_1^2 + 2 s_1 c_1 g_1 g_2 + c_1^2 g_2^2) + g_3^2 \\ &= (c_1^2 + s_1^2) g_1^2 + (s_1^2 + c_1^2) g_2^2 + 0 + g_3^2 \\ &= g_1^2 + g_2^2 + g_3^2 \\ \end{align*} $$非常棒,$c_1$和$s_1$全没了,$\theta_1$被干掉了,这验证了我们的猜想,可以继续计算,并整理成下面的形式:
$$ \begin{align*} r &= g_1^2 + g_2^2 + g_3^2 \\ &= f_1^2 + f_2^2 + f_3^2 + a_1^2 + d_2^2 + 2d_2 f_3 + 2a_1(c_2 f_1 - s_2 f_2) \\ &= (k_1 c_2 + k_2 s_2) 2a_1 + k_3 \end{align*} $$其中$k_1$、$k_2$、$k_3$仅为$\theta_3$的函数:
$$ \begin{aligned} k_1(\theta_3) &= f_1 \\ k_2(\theta_3) &= -f_2 \\ k_3(\theta_3) &= f_1^2 + f_2^2 + f_3^2 + a_1^2 + d_2^2 + 2d_2 f_3 \end{aligned} $$同样地,手腕中心相对地面的高度也与$\theta_1$无关,前面$^0 P_{4 \text{ORG}}$的表达式已经计算出其$z$值与$g_3$相等,而$g_3$是$\theta_2$和$\theta_3$的函数,则符合猜想。下面我们继续计算高度$z$,将其化为与上面的$r$相似的形式:
$$ \begin{aligned} z = g_3 &= (k_1 s_2 - k_2 c_2) s\alpha_1 + k_4 \\ k_4(\theta_3) &= f_3 c\alpha_1 + d_2 c\alpha_1 \end{aligned} $$由此,联立$z$和$r$,我们就有了一个只有$\theta_2$和$\theta_3$的二元方程组:
$$ \begin{cases} r = (k_1 c_2 + k_2 s_2) 2a_1 + k_3 \\ z = (k_1 s_2 - k_2 c_2) s\alpha_1 + k_4 \end{cases} $$我们先考虑一些特殊情况,当$a_1$或$sa_1$等于0时,前一项直接就消除了,则相当于直接将另一个方程与$k_3$或$k_4$联立,由于都是$\theta_3$的函数,可以较快计算出$\theta_3$,这里不多赘述。
如果$a_1$和$sa_1$都不为0,经过一些消元步骤,我们最后能整理出一个类似椭圆方程的关于$\theta_3$的一元方程(这大抵就是数学的魅力吧):
$$ \frac{s\alpha_1 (r - k_3)^2}{4 a_1^2} + \frac{(z - k_4)^2}{s^2\alpha_1} = k_1^2 + k_2^2 $$至此,我们的消元步骤就完成了。
回代
接下来,我们可以直接用高数上就学过的万能公式$\frac{2u}{1 + u^2}$和$\frac{1 - u^2}{1 + u^2}$来代替$\sin\theta_3$和$\cos\theta_3$,当然$u = \tan \left( \frac{\theta_3}{2} \right)$,不难就能解出$\theta_3$的值。然后将$\theta_3$回代到$r = (k_1 c_2 + k_2 s_2) 2a_1 + k_3$中,解出$\theta_2$。最后把$\theta_2$和$\theta_3$统一回代到最初的$x = c_1 g_1 - s_1 g_2$中,解出$\theta_1$(当然代到$y$中也可以)。
到此为止,我们成功从最初的${}^{6}_{0} T$解算出$\theta_1$、$\theta_2$、$\theta_3$,虽然事实上我们只用了${}^{6}_{0} T$的第四列${}^0 P_{6 \text{ORG}}$,所以接下来我们就要用到前三列了。
$\theta_4$、$\theta_5$、$\theta_6$解算
我们解算出$\theta_1$、$\theta_2$、$\theta_3$后,根据DH Craig的定义,可以计算出${}^{3}_{0} R$:
$$ {}_0^3R = {}_0^1R {}_1^2R {}_2^3R = \begin{bmatrix} c_1 & -s_1 & 0 \\ s_1 & c_1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c_2 & -s_2 & 0 \\ s_2 c\alpha_1 & c_2 c\alpha_1 & -s\alpha_1 \\ s_2 s\alpha_1 & c_2 s\alpha_1 & c\alpha_1 \end{bmatrix} \begin{bmatrix} c_3 & -s_3 & 0 \\ s_3 c\alpha_2 & c_3 c\alpha_2 & -s\alpha_2 \\ s_3 s\alpha_2 & c_3 s\alpha_2 & c\alpha_2 \end{bmatrix} $$由于后3个Joint转轴相交,Frame共原点,其只影响转动量,而不影响Frame的原点位置,因此我们只需要${}_3^6R$就可以解算出$\theta_4$、$\theta_5$、$\theta_6$三个角。由于旋转矩阵是正交矩阵,其逆矩阵就等于转置矩阵,根据我们已有的${}_0^6T$提取出${}_0^6R$可以快速计算出${}_3^6R$:
$$ {}_6^3R = {}_3^0R^{-1} \cdot {}_6^0R = {}_3^0R^{T} \cdot {}_6^0R $$接下来可以套用Z-Y-Z欧拉角变换反解算${}_3^6R$的角度,$atan2$函数相当于对应极坐标的极角或对应复数的辐角:
$$ {}^6_3 R_{Z'Y'Z'}(\alpha, \beta, \gamma) = \begin{bmatrix} c\alpha c\beta c\gamma - s\alpha s\gamma & -c\alpha c\beta s\gamma - s\alpha c\gamma & c\alpha s\beta \\ s\alpha c\beta c\gamma + c\alpha s\gamma & -s\alpha c\beta s\gamma + c\alpha c\gamma & s\alpha s\beta \\ -s\beta c\gamma & s\beta s\gamma & c\beta \end{bmatrix}= \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} $$$$ \begin{aligned} \beta &= \text{atan2} \left( \sqrt{r_{31}^2 + r_{32}^2}, r_{33} \right) \\ \alpha &= \text{atan2} \left( \frac{r_{23}}{s\beta}, \frac{r_{13}}{s\beta} \right) \\ \gamma &= \text{atan2} \left( \frac{r_{32}}{s\beta}, \frac{-r_{31}}{s\beta} \right) \end{aligned} $$需要注意的是,这里计算出的$\alpha$、$\beta$、$\gamma$不完全是$\theta_4$、$\theta_5$、$\theta_6$,因为欧拉角变换定义的旋转角是始终沿转动过程中的坐标轴旋转的角度,而DH Craig定义的Joint Angle是两个Frame的x轴之间夹角,虽然两者都是逆时针为正。对于一般情况,x轴定义的方向是Link的方向,但此处三个轴线相交,不存在Links,此时x轴的定义的方向则是同时垂直于当前轴与上一轴轴线的方向,具体可以看下图:
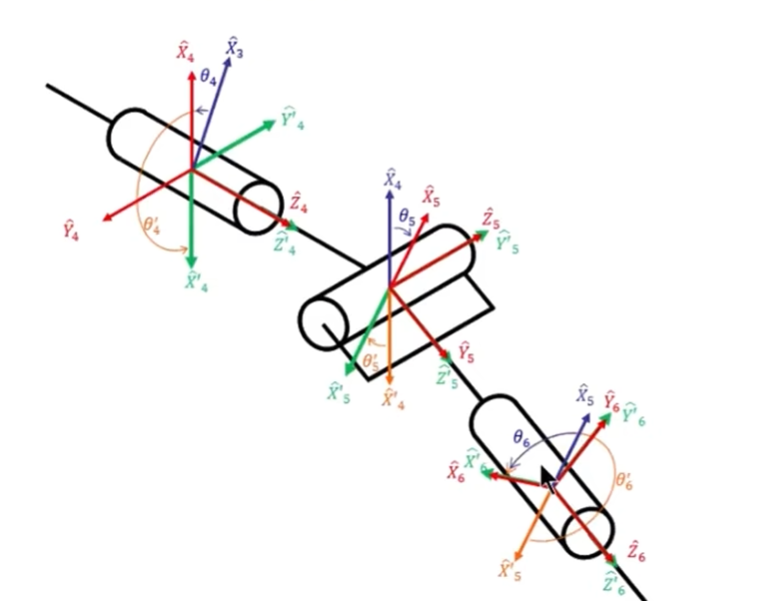
根据此图我们可以发现,在套用Z-Y-Z欧拉角变换时,为了让最终Frame姿态和DH定义的Frame6重合,第一次旋转多转了180°,第二次反转原角度,第三次又多转了180°。因此我们得到:
$$ \begin{aligned} \theta_4 &= \alpha - \pi \\ \theta_5 &= - \beta \\ \theta_6 &= \gamma - \pi \end{aligned} $$到此为止,历经千辛万苦,我们终于成功从一个${}^{6}_{0} T$解算出了$\theta_1$、$\theta_2$、$\theta_3$、$\theta_4$、$\theta_5$、$\theta_6$六个角度,光理解这个计算过程我已经用尽全身气力,真是佩服Craig、Pieper这些开山鼻祖,人类的智慧还是太强大了!
两张图片和计算思想基本来自台大林沛群的课程。